A Very Short Introduction to Artificial Neural Networks

  As mentioned above, our simulations utilized the ``multi layered perceptron model'' (MLP), also known as ``feed forward networks'' trained with the ``generalized delta rule'', also known as ``backpropagation''.

The foundations of the backpropagation method for learning in neural networks were laid by [RHW86].

Artificial neural networks consist of many simple processing devices (called processing elements or neurons) grouped in layers. Each layer is identified by the index $l=0,\ldots,L$. The layers and L are called the ``input layer'' and ``output layer'', all other layers are called ``hidden layers''. The processing elements are interconnected as follows: Communication between processing elements is only allowed for processing elements of neighbouring layers. Neurons within a layer cannot communicate. Each neuron has a certain activation level a. The network processes data by the exchange of activation levels between connected neurons (see figure 1):

 

Figure:   Exchange of activation values between neurons

The output value of the i-th neuron in layer l is denoted by x_i^(l). It is calculated with the formula

x_i^(l) = g(a_i^(l))

where $g(\cdot)$ is a monotone increasing function. For our examples, we use the function $g(y)=\frac{1}{1 + e^{-y}}$ (the ``squashing function''). The activation level a_i^(l) of the neuron i in layer l is calculated by

a_i^(l) = f(u_i^(l))

where $f(\cdot)$ is the activation function (in our case the identity function is used).

The net input u_i^(l) of neuron i in layer l is calculated as

$$u_i^{(l)} = \biggl( \sum_{j = 1}^{n^{(l-1)}} {w_{ij}^{(l)} x_j^{(l-1)} \biggr)} - \Theta_i^{(l)}$$

where w_ij^(l) is the weight of neuron j in layer l-1 connected to neuron i in layer l, x_j^(l-1) is the output of neuron j in layer l-1. $\Theta_i^{(l)}$ is a bias value that is subtracted from the sum of the weighted activations.

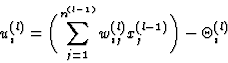
The calculation of the network status starts at the input layer and ends at the output layer. The input vector I initializes the activation levels of the neurons in the input layer:

$$a^{(0)}_i = {\rm i^{\rm th}~element~of~I}$$

For the input layer, $g(\cdot)$ is the identity function. The activation level of one layer is propagated to the next layer of the network. Then the weights between the neurons are changed by the backpropagation learning rule. The artificial neural network learns the input/output mapping by a stepwise change of the weights and minimizes the difference between the actual and desired output vector.

The simulation can be divided into two main phases during network training: A randomly selected input/output pair is presented to the input layer of the network. The activation is then propagated to the hidden layers and finally to the output layer of the network.

In the next step the actual output vector is compared with the desired result. Error values are assigned to each neuron in the output layer. The error values are propagated back from the output layer to the hidden layers. The weights are changed so that there is a lower error for a new presentation of the same pattern. The so called ``generalized delta rule'' is used as learning procedure in multi layered perceptron networks.

The weight change in layer l at time v is calculated by

$$\Delta w_{ij}^{(l)}(v) = \eta \delta_i^{(l)} x_j^{(l-1)} + \alpha \Delta w_{ij}^{(l)}(v-1)$$

where $\eta\in(0,1)$ is the learning rate and $\alpha\in(0,1)$ is the momentum. Both are kept constant during learning. $\delta_i^{(l)}$ is defined

1.

for the output layer (l = L) $\delta_i^{(L)}$ as

$$\delta_i^{(L)} = (d_i - x_i^{(L)}) g'(u_i^{(L)})$$

where g'(u_i^(L)) is the gradient of the output function at u_i^(L).The gradient of the output function is always positive.

 

Figure 2:   Weight adaptation between two neurons

The formula can be explained as follows: When the output x_k^(l) of the neuron i in layer l is too small, $\delta_k^{(l)}$ has a negative value. Hence the output of the neuron can be raised by increasing the net input u_k^(l) by the following change of the weight values:

if x_i^(l-1) > 0, then increase w_ki^(l)

if x_i^(l-1) < 0, then decrease w_ki^(l)

The rule applies vice versa for a neuron with an output value that is too high (see figure 2).

2.

for all neurons underneath the output layer (l < L) $\delta_i^{(l)}$ is defined by:

$$\delta_i^{(l)} = g'(u_i^{(l)}) \sum_{k=1}^{n^{(l+1)}} \delta_k^{(l+1)} w_{ki}^{(l+1)}$$

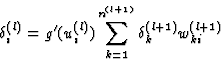
Finally the weights of layer l are adjusted by

$$w_{ij}^{(l,{\rm new})} = w_{ij}^{(l)} + \Delta w_{ij}^{(l)}(v)$$