

Next: Comparison with ARIMA Modeling
Up: Modeling
Previous: The Algorithm
The following parameters of the artificial neural network were chosen
for a closer inspection:
To examine the distribution of these parameters, we conducted a number
of experiments: In subsequent runs of the network, these parameters
were systematically changed to explore their effect on the network's
modeling and forecasting capabilities.
We used the following terms to measure the modeling quality sm and
forecasting quality sf of our system: For a time series
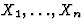
| 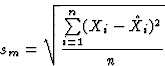 |
(1) |
| 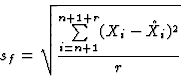 |
(2) |
where 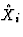 is the estimate of the artificial neural network for
period i and r is the number of forecasting periods. The error
sm (equation 1) estimates the capability of the neural
network to mimic the known data set, the error sf (equation
2) judges the networks's forecast capability for a forecast
period of length r. In our experiments, we used r=20.
is the estimate of the artificial neural network for
period i and r is the number of forecasting periods. The error
sm (equation 1) estimates the capability of the neural
network to mimic the known data set, the error sf (equation
2) judges the networks's forecast capability for a forecast
period of length r. In our experiments, we used r=20.
Note: For reasons of clarity, in this section we only present graphics
for the IBM share price time series. The graphics for the airline
passenger time series are very similar.
The figures 7 and 8
demonstrate the effect of variations of the learning rate 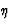 and the momentum
and the momentum 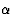 on the modeling (figure
7) and forecast (figure
8) quality: both graphics give evidence for the
robustness of the backpropagation algorithm, high values of both
on the modeling (figure
7) and forecast (figure
8) quality: both graphics give evidence for the
robustness of the backpropagation algorithm, high values of both
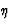 and
and 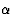 should be avoided.
should be avoided.
Figure:
Learning rate and momentum, IBM share
price, modeling quality
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsfbox [0 247 595 842]{excel/reibmeaw.eps}
}\end{figure}](img36.gif) |
Figure:
Learning rate and momentum, IBM share
price, forecasting quality
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmeap.eps}
}\end{figure}](img37.gif) |
The figures 10 and 11 present
the effect of different network topologies on the modeling (figure
10) and forecasting (figure
11) quality: The number of input units
and the number of hidden units open an interesting view:
artificial neural networks with more than approx. 50 hidden units are
not suited for the task of time series forecasting. This tendency of
``over-elaborate networks capable of data-miming'' is also reported by
[Whi88].
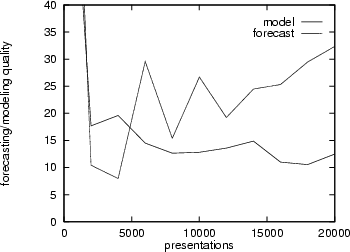
Another parameter we have to consider is the number of presentations.
A longer training period does not necessarily result in a better
forecasting capability. Figure 9 demonstrates this
``overlearning'' effect for the IBM share price time series: with an
increasing number of presentations, the network memorizes details of
the time series data instead of learning its essential features. This
loss of generalization power has a negative effect on the network's
forecasting ability.
Figure 9:
Modeling vs. forecasting ability
 |
These estimations of the network's most important parameters, although
rough, allowed us to choose reasonable parameters for our performance
comparison with the ARIMA technique, described in the next section.
Figure:
Number of input and hidden units, IBM
share price, modeling quality
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmihw.eps}
}\end{figure}](img39.gif) |
Figure:
Number of input and hidden units, IBM
share price, forecasting quality
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmihp.eps}
}\end{figure}](img40.gif) |


Next: Comparison with ARIMA Modeling
Up: Modeling
Previous: The Algorithm
![]() (
(![]() ) is a scaling factor that tells the learning
algorithm how strong the weights of the connections should be
adjusted for a given error. A higher
) is a scaling factor that tells the learning
algorithm how strong the weights of the connections should be
adjusted for a given error. A higher ![]() can be used to speed up
the learning process, but if
can be used to speed up
the learning process, but if ![]() is too high, the algorithm will
``step over'' the optimum weights. The learning rate
is too high, the algorithm will
``step over'' the optimum weights. The learning rate ![]() is
constant across presentations.
is
constant across presentations.
![]() (
(![]() ) is another number
that affects the gradient descent of the weights: To prevent each
connection from following every little change in the solution space
immediately, the momentum term is added that keeps the direction of
the previous step [HKP91], thus avoiding the descent
into local minima. The momentum term is constant across
presentations.
) is another number
that affects the gradient descent of the weights: To prevent each
connection from following every little change in the solution space
immediately, the momentum term is added that keeps the direction of
the previous step [HKP91], thus avoiding the descent
into local minima. The momentum term is constant across
presentations.
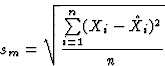
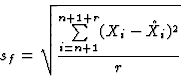
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsfbox [0 247 595 842]{excel/reibmeaw.eps}
}\end{figure}](img36.gif)
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmeap.eps}
}\end{figure}](img37.gif)

![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmihw.eps}
}\end{figure}](img39.gif)
![\begin{figure}
\epsfxsize=80mm\epsfysize=80mm
\centerline{
\epsffile [0 247 595 842]{excel/reibmihp.eps}
}\end{figure}](img40.gif)